标准库(4)
heapq
堆(heap),是一种数据结构。用维基百科中的说明:
堆(英语:heap),是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。
对于这个新的概念,读者不要感觉心慌意乱或者恐惧,因为它本质上不是新东西,而是在我们已经熟知的知识基础上的扩展。
堆的实现是通过构造二叉堆,也就是一种二叉树。
基本知识
这是一颗在苏州很常见的香樟树,马路两边、公园里随处可见。
但是,在编程中,我们常说的树通常不是上图那样的,而是这样的:
跟真实现实生活中看到的树反过来,也就是“根”在上面。为什么这样呢?我想主要是画着更方便吧。但是,我觉这棵树,是完全写实的作品。我本人做为一名隐姓埋名多年的抽象派画家,不喜欢这样的树,我画出来的是这样的:
这棵树有两根枝杈,可不要小看这两根枝杈哦,《道德经》上不是说“一生二,二生三,三生万物”。一就是下面那个干,二就是两个枝杈,每个枝杈还可以看做下一个一,然后再有两个枝杈,如此不断重复(这简直就是递归呀),就成为了一棵大树。
我的确很佩服我自己的后现代抽象派的作品。但是,我更喜欢把这棵树画成这样:
并且给它一个正规的名字:二叉树
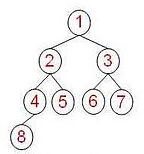
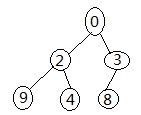
这个也是二叉树,完全脱胎于我所画的后现代抽象主义作品。但是略有不同,这幅图在各个枝杈上显示的是数字。这种类型的“树”就编程语言中所说的二叉树,维基百科曰:
在计算机科学中,二叉樹(英语:Binary tree)是每個節點最多有兩個子樹的樹結構。通常子樹被稱作「左子樹」(left subtree)和「右子樹」(right subtree)。二叉樹常被用於實現二叉查找樹和二叉堆。
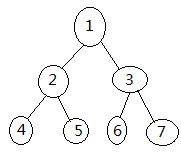
在上图的二叉树中,最顶端的那个数字就相当于树根,也就称作“根”。每个数字所在位置成为一个节点,每个节点向下分散出两个“子节点”。就上图的二叉树,在最后一层,并不是所有节点都有两个子节点,这类二叉树又称为完全二叉树(Complete Binary Tree),也有的二叉树,所有的节点都有两个子节点,这类二叉树称作满二叉树(Full Binarry Tree),如下图:
下面讨论的对象是实现二叉堆就是通过二叉树实现的。其应该具有如下特点:
- 节点的值大于等于(或者小于等于)任何子节点的值。
- 节点左子树和右子树是一个二叉堆。如果父节点的值总大于等于任何一个子节点的值,其为最大堆;若父节点值总小于等于子节点值,为最小堆。上面图示中的完全二叉树,就表示一个最小堆。
堆的类型还有别的,如斐波那契堆等,但很少用。所以,通常就将二叉堆也说成堆。下面所说的堆,就是二叉堆。而二叉堆又是用二叉树实现的。
堆的存储
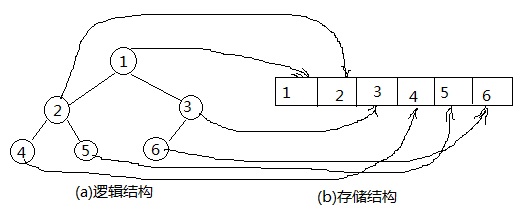
堆用列表(有的语言中成为数组)来表示。如下图所示:
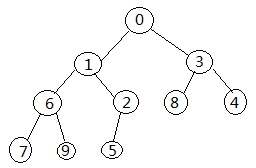
从图示中可以看出,将逻辑结构中的树的节点数字依次填入到存储结构中。看这个图,似乎是列表中按照顺序进行排列似的。但是,这仅仅由于那个树的特点造成的,如果是下面的树:
如果将上面的逻辑结构转换为存储结构,读者就能看出来了,不再是按照顺序排列的了。
关于堆的各种,如插入、删除、排序等,本节不会专门讲授编码方法,读者可以参与有关资料。但是,下面要介绍如何用python中的模块heapq来实现这些操作。
heapq模块
heapq中的heap是堆,q就是queue(队列)的缩写。此模块包括:
>>> import heapq
>>> heapq.__all__
['heappush', 'heappop', 'heapify', 'heapreplace', 'merge', 'nlargest', 'nsmallest', 'heappushpop']依次查看这些函数的使用方法。
heappush(heap, x):将x压入对heap(这是一个列表)
Help on built-in function heappush in module _heapq:
heappush(...)
heappush(heap, item) -> None. Push item onto heap, maintaining the heap invariant.
>>> import heapq
>>> heap = []
>>> heapq.heappush(heap, 3)
>>> heapq.heappush(heap, 9)
>>> heapq.heappush(heap, 2)
>>> heapq.heappush(heap, 4)
>>> heapq.heappush(heap, 0)
>>> heapq.heappush(heap, 8)
>>> heap
[0, 2, 3, 9, 4, 8]请读者注意我上面的操作,在向堆增加数值的时候,我并没有严格按照什么顺序,是随意的。但是,当我查看堆的数据时,显示给我的是一个有一定顺序的数据结构。这种顺序不是按照从小到大,而是按照前面所说的完全二叉树的方式排列。显示的是存储结构,可以把它还原为逻辑结构,看看是不是一颗二叉树。
由此可知,利用heappush()函数将数据放到堆里面之后,会自动按照二叉树的结构进行存储。
heappop(heap):删除最小元素
承接上面的操作:
>>> heapq.heappop(heap)
0
>>> heap
[2, 4, 3, 9, 8]用heappop()函数,从heap堆中删除了一个最小元素,并且返回该值。但是,这时候的heap显示顺序,并非简单地将0去除,而是按照完全二叉树的规范重新进行排列。
heapify():将列表转换为堆
如果已经建立了一个列表,利用heapify()可以将列表直接转化为堆。
>>> hl = [2, 4, 6, 8, 9, 0, 1, 5, 3]
>>> heapq.heapify(hl)
>>> hl
[0, 3, 1, 4, 9, 6, 2, 5, 8]经过这样的操作,列表hl就变成了堆(注意观察堆的顺序,和列表不同),可以对hl(堆)使用heappop()或者heappush()等函数了。否则,不可。
>>> heapq.heappop(hl)
0
>>> heapq.heappop(hl)
1
>>> hl
[2, 3, 5, 4, 9, 6, 8]
>>> heapq.heappush(hl, 9)
>>> hl
[2, 3, 5, 4, 9, 6, 8, 9]不要认为堆里面只能放数字,之所以用数字,是因为对它的逻辑结构比较好理解。
>>> heapq.heappush(hl, "q")
>>> hl
[2, 3, 5, 4, 9, 6, 8, 9, 'q']
>>> heapq.heappush(hl, "w")
>>> hl
[2, 3, 5, 4, 9, 6, 8, 9, 'q', 'w']heapreplace()
是heappop()和heappush()的联合,也就是删除一个,同时加入一个。例如:
>>> heap
[2, 4, 3, 9, 8]
>>> heapq.heapreplace(heap, 3.14)
2
>>> heap
[3, 4, 3.14, 9, 8]先简单罗列关于对的几个常用函数。那么堆在编程实践中的用途在哪方面呢?主要在排序上。一提到排序,读者肯定想到的是sorted()或者列表中的sort(),不错,这两个都是常用的函数,而且在一般情况下已经足够使用了。如果再使用堆排序,相对上述方法应该有优势。
堆排序的优势不仅更快,更重要的是有效地使用内存,当然,另外一个也不同忽视,就是简单易用。比如前面操作的,删除数列中最小的值,就是在排序基础上进行的操作。
deque模块
有这样一个问题:一个列表,比如是[1,2,3],我打算在最右边增加一个数字。
这也太简单了,不就是用append()这个内建函数,追加一个吗?
这是简单,我要得寸进尺,能不能在最左边增加一个数字呢?
这个嘛,应该有办法。不过得想想了。读者在向下阅读的时候,能不能想出一个方法来?
>>> lst = [1, 2, 3]
>>> lst.append(4)
>>> lst
[1, 2, 3, 4]
>>> nl = [7]
>>> nl.extend(lst)
>>> nl
[7, 1, 2, 3, 4]你或许还有别的方法。但是,python为我们提供了一个更简单的模块,来解决这个问题。
>>> from collections import deque这次用这种引用方法,因为collections模块中东西很多,我们只用到deque。
>>> lst
[1, 2, 3, 4]还是这个列表。试试分别从右边和左边增加数
>>> qlst = deque(lst)这是必须的,将列表转化为deque。deque在汉语中有一个名字,叫做“双端队列”(double-ended queue)。
>>> qlst.append(5) #从右边增加
>>> qlst
deque([1, 2, 3, 4, 5])
>>> qlst.appendleft(7) #从左边增加
>>> qlst
deque([7, 1, 2, 3, 4, 5])这样操作多么容易呀。继续看删除:
>>> qlst.pop()
5
>>> qlst
deque([7, 1, 2, 3, 4])
>>> qlst.popleft()
7
>>> qlst
deque([1, 2, 3, 4])删除也分左右。下面这个,请读者仔细观察,更有点意思。
>>> qlst.rotate(3)
>>> qlst
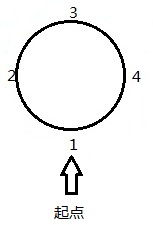
deque([2, 3, 4, 1])rotate()的功能是将[1, 2, 3, 4]的首位连起来,你就想象一个圆环,在上面有1,2,3,4几个数字。如果一开始正对着你的是1,依顺时针方向排列,就是从1开始的数列,如下图所示:
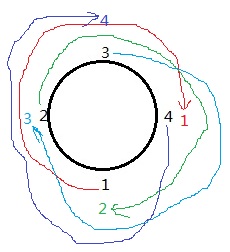
经过rotate(),这个环就发生旋转了,如果是rotate(3),表示每个数字按照顺时针方向前进三个位置,于是变成了:
请原谅我的后现代注意超级抽象派作图方式。从图中可以看出,数列变成了[2, 3, 4, 1]。rotate()作用就好像在拨转这个圆环。
>>> qlst
deque([3, 4, 1, 2])
>>> qlst.rotate(-1)
>>> qlst
deque([4, 1, 2, 3])如果参数是复数,那么就逆时针转。
在deque中,还有extend和extendleft方法。读者可自己调试。